Module on Adaptive Experimentation

Human-Centered Data Science gives us new ways to analyze and apply data. We can combine ideas from traditional experiments with machine learning methods to do an adaptive experiment.

In an adaptive experiment, we adjust our design — typically the allocation of participants to different conditions — based on what we learn from each interaction with participants at any given point. The goal is usually to balance exploration — testing various conditions to gather more information about their effectiveness with exploitation — using the algorithm’s knowledge so far to allocate participants to the currently better-performing conditions.

One example of balancing exploration and exploitation is finding good restaurants in a new city. At first, you explore different options, trying various places to gather information about what’s good. Once you’ve identified a standout spot, you start visiting it more often, but still occasionally try new places in case there’s an even better one you haven’t discovered yet.

One strategy to achieve balancing exploration and exploitation in practice is is response-adaptive randomization, where the probabilities of assigning participants to each condition are adjusted based on accumulated evidence. As more data from participants is gathered over time, the allocation approach gradually shifts away from an even split (e.g., 50/50) toward favoring conditions that perform better empirically based on the available evidence.

Question:

Could you suggest another example illustrating the idea of an adaptive experiment?

Thanks for Response! Another example to think of is to test the effectiveness of two type of vaccines.

Question:

Select a true statement about randomization.

Response-adaptive randomization always starts from unequal probabilities of assignment for each condition.Traditional (uniform-randomly assigned) experiments express our preference toward exploration compared to exploitation.The goal of response-adaptive randomization is to achieve equal size of groups for each condition.Randomization always assumes equal probabilities of assignment to conditions.

Randomization always assumes equal probabilities of assignment to conditions:

Explanation of Options:

• Option 1: False. Response-adaptive randomization typically begins with equal probabilities and adjusts them based on participant responses, rather than always starting with unequal probabilities.

• Option 2: True. Traditional uniform randomization assigns participants equally across all conditions, reflecting a preference for exploration by ensuring that all conditions are equally tested without bias toward any particular option.

• Option 3: False. The goal of response-adaptive randomization is to allocate more participants to better-performing conditions based on interim results, not necessarily to achieve equal group sizes.

• Option 4: False. While traditional randomization assumes equal probabilities of assignment, response-adaptive randomization may use unequal probabilities based on ongoing results, so randomization does not always assume equal probabilities.

Let’s recap some definitions

Condition: A specific treatment, arm, or variation assigned to a participant during the experiment.

Reward: A measurable outcome or benefit that results from a participant’s interaction with one of the conditions. In the simplest case, the reward can be binary: a success or a failure, e.g., answering a test question correctly or not.

Response-adaptive randomization: A method used in experiments where the probability of assigning participants to different conditions changes over time based on observed results (e.g. reward).

Adaptive experiment is a type of randomized trial (for example, in areas like clinical trials, and educational research) in which we adjust our design — typically the allocation to different conditions — based on what we learn from interactions with participants. In this module, we will focus on adaptive experiments using statistical and machine learning methods to perform response-adaptive randomization.

Question:

Developing your example of an adaptive experiment from the task above, suggest conditions for your example. Feel free to discuss alternative ideas.

Thank you for your response! Example conditions could include two types of treatments such as:

1. Vaccine A with a higher initial dosage.
   
2. Vaccine B with a standard dosage and booster after one month.

These conditions would allow for comparing the effectiveness and adaptively assigning participants based on observed outcomes.

Question:

Developing your example of an adaptive experiment from the task above, suggest a reward for your example. Feel free to discuss alternative ideas.

Thank you for your response! An example reward could be whether an individual participant survives after receiving the treatment (mortality). Alternatively, it could measure improvements in the participant’s health, such as reduced symptom severity or time to recovery.

Question:

Which of the following statements about adaptive experiments is correct?

Adaptive experiments are not usually randomized.Adaptive experiments are not usually uniformly randomized.Adaptive experiments ensure an even split of participants across all conditions throughout the experiment.The primary goal of adaptive experiments is to avoid randomization entirely.

Adaptive experiments are not usually uniformly randomized:

Explanation of Options:

• Option 1: False. Adaptive experiments often involve randomization, but the randomization is adjusted dynamically based on prior responses.

• Option 2: True. Adaptive experiments typically deviate from uniform randomization, dynamically adjusting the allocation probabilities based on observed data to optimize outcomes.

• Option 3: False. Adaptive experiments do not aim to ensure an even split of participants across conditions; instead, they aim to allocate participants based on performance or other criteria.

• Option 4: False. The primary goal of adaptive experiments is to improve efficiency and outcomes, not to eliminate randomization entirely.

Question:

Which of the following statements about adaptive experiments is correct?

Response-adaptive randomization always requires observing rewards immediately.Rewards in adaptive experiments are always binary, representing success or failure.One condition in adaptive experiments should always be control.To update the probabilities of assigning the participants to different conditions, we have to observe rewards.

To update the probabilities of assigning the participants to different conditions, we have to observe rewards:

Explanation of Options:

• Option 1: False. While observing rewards is necessary for updating probabilities, the observation does not always need to be immediate; delayed rewards can also be incorporated into adaptive randomization.

• Option 2: False. Rewards in adaptive experiments can take various forms, such as continuous values, ordinal scales, or other metrics, not just binary success/failure.

• Option 3: False. Adaptive experiments do not necessarily require a control condition; they can involve multiple experimental conditions with no distinct control group.

• Option 4: True. Observing rewards is essential for updating the allocation probabilities in adaptive experiments, as the reward feedback informs how conditions are adjusted dynamically.

WALKTHROUGH

How response-adaptive randomization works step-by-step:

Let’s illustrate on a simple example, tracing adaptive experiment throughout three steps:

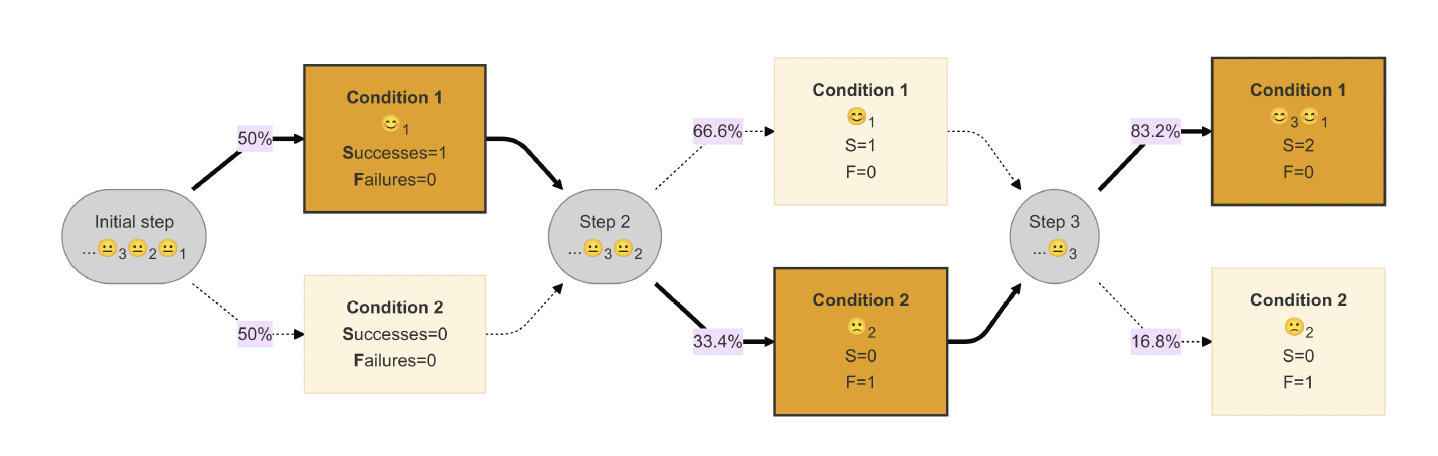Initial Step:

1. • The experiment begins with a group of participants (…🙂₃🙂₂🙂₁)

   • Participants are randomly assigned with a 50-50 probability:

     • Condition 1: Selected by the algorithm (highlighted arrow), and participant gave us a positive reward 🙂₁. We updated our success counter (S=1, F=0).

     • Condition 2: Not selected (non-highlighted arrow), with no outcomes yet (S=0, F=0).

Step 2:

• Next participant from our pool (…🙂₃🙂₂) proceeds.

• Based on updated probabilities (67% and 33%), the algorithm randomly assigns a Condition for the next participant:

  • Condition 1: Despite 67% probability of assignment, the algorithm does not select this condition this time. We still have (S=1, F=0)

  • Condition 2: With 33% probability of assignment, we selected Condition 2 for a participant, but they didn’t like it (🙂₂). We updated our failure counter (S=0, F=1).

Step 3:

• The next participant in our pool (…🙂₃) proceeds.

• Probabilities of assignment are adjusted again based on previous outcomes (83% for Condition 1, 17% for Condition 2):

  • Condition 1: With an 83% probability of assignment, the algorithm indeed selects Condition 1 this time, and the participant responded positively (🙂₃). We update our success counter to (S=2, F=0).

  • Condition 2: Despite that we still could have selected this condition (with 17% probability), we did not, so we make no updates to this condition, and it remains at (S=0, F=1).

After the three steps we have:

• Condition 1 (S=2, F=0), probability of assignment 90%
• Condition 2 (S=0, F=1), probability of assignment 10%

Question:

After Step 3, we can definitively conclude that Condition 1 is really better than Condition 2.

FalseTrue

False:

Explanation of Options:

• Option 1 (False): Correct. After Step 3, conclusions about the superiority of Condition 1 over Condition 2 cannot be definitively made. Adaptive experiments often require additional data or steps to confirm such claims with statistical confidence.

• Option 2 (True): Incorrect. Conclusions about superiority require rigorous statistical evidence and may not be definitively established after just Step 3, as further steps or validation are typically needed.

Question:

After Step 3, our reward statistics were the following: - Condition 1 (S=2, F=0), probability of assignment 90% - Condition 2 (S=0, F=1), probability of assignment 10%

If on the next step (Step 4) we select Condition 2 for the next participant and get a positive reward, the reward statistics will be updated this way:

Condition 2 (S=0, F=2)Condition 2 (S=1, F=1)Condition 1 (S=1, F=1)Condition 1 (S=2, F=1)

Condition 2 (S=1, F=1):

Explanation of Options:

• Option 1: Incorrect. If a positive reward is observed for Condition 2, the success count (S) should increase, not the failure count (F).

• Option 2: Correct. When a positive reward is observed for Condition 2, the statistics are updated to reflect one success (S=1) and one failure (F=1).

• Option 3: Incorrect. This option mixes up Condition 1’s statistics, which should remain unchanged as it was not selected in Step 4.

• Option 4: Incorrect. A positive reward does not affect the failure count (F) of Condition 1 or Condition 2.

Question:

If on Step 4 we selected Condition 2 for the next participant and got a positive reward, after Step 4:

Condition 2 would more likely be selected than Condition 1.Condition 1 would more likely be selected than Condition 2.Both conditions are equally likely to be selected.

Condition 1 would more likely be selected than Condition 2:

Explanation of Options:

• Option 1: Incorrect. Although Condition 2 received a positive reward, Condition 1 already has a stronger history of success, making it more likely to be selected.

• Option 2: Correct. Condition 1, with its stronger historical reward statistics, remains the more likely choice for selection despite Condition 2’s positive reward in Step 4.

• Option 3: Incorrect. The probabilities of selection are updated dynamically based on reward statistics, and the conditions are unlikely to have equal probabilities unless their performance metrics align perfectly.

Question:

If on Step 4 we selected Condition 2 for the next participant and got a positive reward, after Step 4:

We believe that Condition 1 would be more likely to fail on the following step.We believe that Condition 2 would be equally likely to bring success or failure.We believe that Condition 1 would be equally likely to bring success or failure.We believe that Condition 2 would be more likely to fail on the following step.

We believe that Condition 2 would be equally likely to bring success or failure:

Explanation of Options:

• Option 1: Incorrect. Condition 1’s likelihood of failure isn’t directly inferred from the performance of Condition 2 in this context.

• Option 2: Correct. After a positive reward for Condition 2, we update our belief, and the posterior distribution for Condition 2 becomes centered around equal success and failure probabilities, assuming prior uniformity.

• Option 3: Incorrect. There’s no reason to update Condition 1’s statistics or belief as it was not selected on Step 4.

• Option 4: Incorrect. A positive reward for Condition 2 suggests that it is not more likely to fail on the next step, rather it maintains a balanced likelihood.

LEARN MORE

Technical Note: Probability of Assignment (or Selection)

In this introduction, we omit the technical details of how probability distributions for each condition are used to select a condition at each step of the algorithm. It is sufficient to understand that we can calculate the probability of assignment (or selection) for each condition at every step, reflecting our current understanding of the relative effectiveness of each condition. For a binary reward (e.g., success or failure), these probabilities are based on the observed numbers of successes and failures for each condition.

The probability of assignment reflects not only the average effectiveness of each condition but also our uncertainty about this effectiveness. Early in an adaptive experiment, when we have limited information or when the effectiveness data fluctuates significantly, the assignment probabilities account for this uncertainty by encouraging more exploration to better understand each condition.

We can observe changes in uncertainty by examining the proportion of allocation to conditions over time. In the graph below, the allocation to conditions remains constant during a traditional Randomized Controlled Trial (RCT) but varies in an adaptive experiment. During the early stages of the adaptive experiment, uncertainty about the effectiveness of the conditions is higher, leading to more reallocation and fluctuations. As the adaptive experiment progresses, our understanding improves, resulting in more stable allocation probabilities.

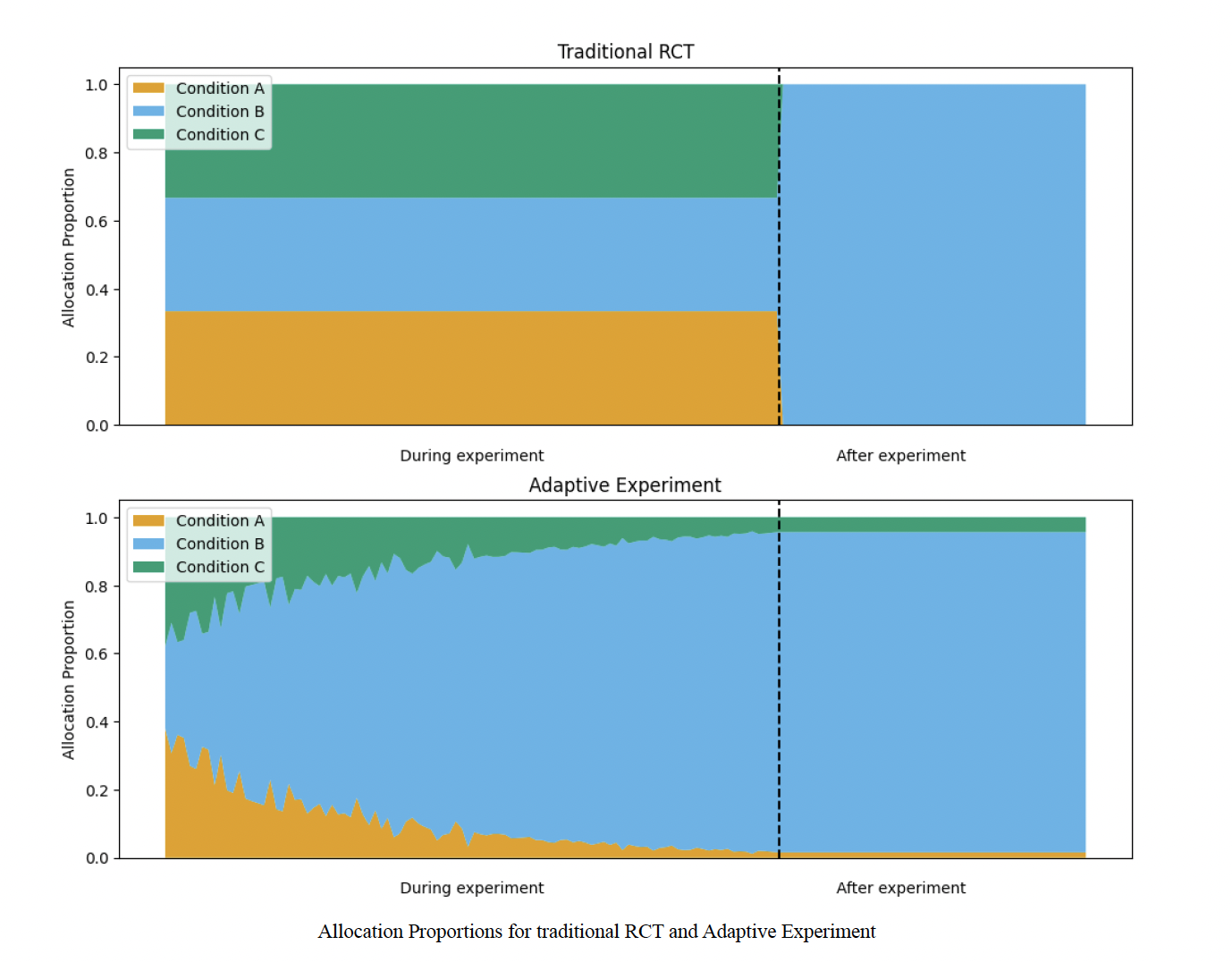
Question:

Increasing allocation proportion for Condition B on the graph for an adaptive experiment reflects:

Increasing exploitation of a better condition based on accumulated evidence.Maintaining equal allocation among all conditions to avoid bias in accumulated evidence.Increasing exploration of conditions to gather more accumulated evidence.

Increasing exploitation of a better condition based on accumulated evidence:

Explanation of Options:

• Option 1: Correct. The increasing allocation proportion for Condition B indicates that the algorithm is prioritizing this condition, exploiting it as evidence accumulates that it is the better-performing condition.

• Option 2: Incorrect. Adaptive experiments do not aim to maintain equal allocation; instead, they adjust allocation to reflect evidence and favor better-performing conditions.

• Option 3: Incorrect. An increasing allocation proportion does not reflect exploration; rather, it represents exploitation of the condition that has demonstrated better performance based on accumulated evidence.

Question:

Which statement about the probability of selection in adaptive experiments is correct?

Conditions with fewer participants are always more likely to be selected to ensure even group sizes.The more relative successes we observe for the condition, the higher the probability of selection for this condition.The probability of selection is determined before the experiment and does not change.The probability of selection remains constant throughout the adaptive experiment, regardless of observed rewards for the conditions.

The more relative successes we observe for the condition, the higher the probability of selection for this condition:

Explanation of Options:

• Option 1: Incorrect. Selection probability is not solely determined by the number of participants in each condition; it depends on the observed successes and failures.

• Option 2: Correct. Adaptive experiments dynamically adjust selection probabilities based on relative successes, increasing the likelihood of selecting better-performing conditions.

• Option 3: Incorrect. Selection probabilities are not fixed before the experiment; they are updated as new data is observed.

• Option 4: Incorrect. In adaptive experiments, selection probabilities change in response to observed rewards, reflecting the current understanding of condition performance.

Question:

What influences the probability of selection in adaptive experiments?

The probability of selection depends on our current knowledge about the effectiveness of every condition.The probability of selection is based solely on initial randomization ratios for the conditions.The probability of selection depends solely on the number of participants assigned to a condition.It is always enough to know how effective the best condition is to calculate the probability of selection.

The probability of selection depends on our current knowledge about the effectiveness of every condition:

Explanation of Options:

• Option 1: Correct. Adaptive experiments dynamically adjust selection probabilities based on the accumulated knowledge of each condition’s effectiveness.

• Option 2: Incorrect. Initial randomization ratios may provide a starting point, but selection probabilities are updated throughout the experiment as new evidence is gathered.

• Option 3: Incorrect. Selection probabilities are not determined solely by the number of participants; they also incorporate effectiveness metrics.

• Option 4: Incorrect. Knowing the effectiveness of only the best condition is insufficient; selection probabilities require information about all conditions to balance exploration and exploitation.

Now, let us try to summarize how one version of an adaptive experiment algorithm might work:

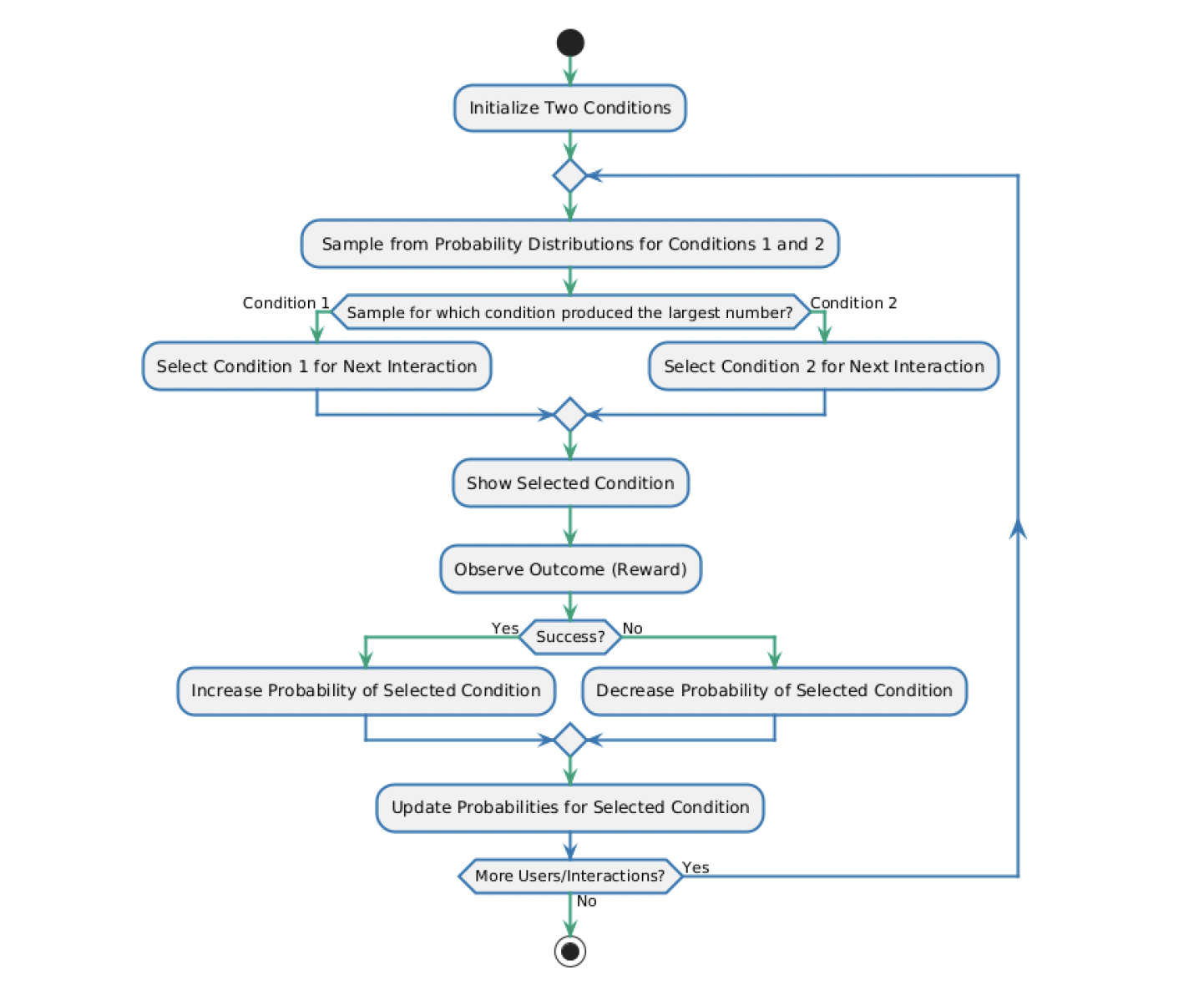
Question:

Based on the walkthrough and the algorithm above, select the correct answer:

At the end of our experiment, one of the conditions will always have 100% probability of assignment.Using probabilities of selection instead of deterministic rules allows adaptive experiments to flexibly balance exploration and exploitation.An adaptive experiment always selects the condition with the highest probability of selection.We always observe a positive reward (success) for the condition with the highest probability of selection.

Using probabilities of selection instead of deterministic rules allows adaptive experiments to flexibly balance exploration and exploitation:

Explanation of Options:

• Option 1: Incorrect. At the end of the experiment, conditions may still have varying probabilities of assignment, but no condition is guaranteed to have 100% probability.

• Option 2: Correct. Adaptive experiments leverage probabilistic selection to balance the need to explore conditions with the need to exploit the best-performing ones.

• Option 3: Incorrect. Adaptive experiments do not always select the condition with the highest probability; the selection is probabilistic and not deterministic.

• Option 4: Incorrect. Observing a positive reward for the condition with the highest probability is not guaranteed, as rewards depend on real-world outcomes, which may vary.

So when do we stop the experiment?

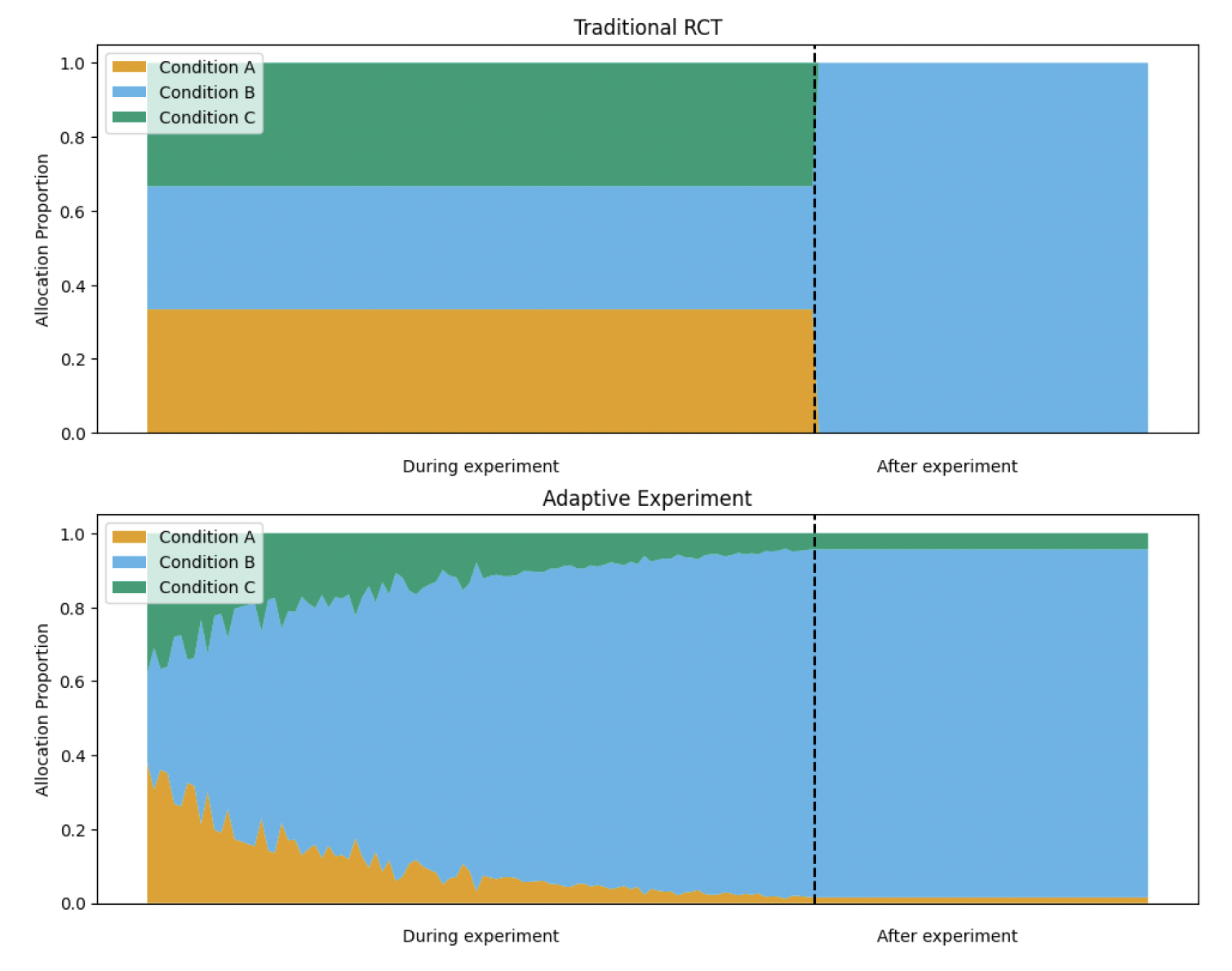
Looking at the graph, we can ask ourselves: “When should we stop an adaptive experiment? What is the dividing line between ‘during’ and ‘after’?”

There are three possible answers:

1. Never.
   If the adaptive experiment is going well, it can serve as an automated decision-making tool, balancing the exploitation of a better condition with the exploration of alternatives in proportion to uncertainty. In this scenario, it is even possible to introduce a new condition and let the algorithm learn how it performs while continuing to use the knowledge gathered from previous conditions.

2. When the sample is complete.
   Adaptive experiments are often used when we need to balance exploitation with exploration within a limited sample. At the end of the experiment, we can examine the final assignment probabilities and interpret them as estimates of the probability of superiority for each condition. These probabilities provide insights beyond just predicting the next step—they help identify which condition is actually better.

3. Based on power analysis.
   Similar to traditional Randomized Controlled Trials (RCTs), we can calculate the sample size required to achieve a target level of statistical power. After obtaining a sufficiently large sample, statistical analysis can be applied to the results of the adaptive experiment.

Each of these approaches has its limitations, and the choice of when to stop an adaptive experiment ultimately depends on the researcher’s judgment and the specific context of the study.

EXAMPLE

Full Example of an Adaptive Experiment

Now that we have some understanding of adaptive experiments, let’s examine a real-world-inspired example. This example will focus on analyzing results and comparing outcomes between a traditional uniformly-randomly assigned Randomized Controlled Trial (RCT) and an adaptive experiment.

Learning designer Yi wants to encourage student self-reflection after course activities. Her goal is to help students think critically about their responses and learning processes.

Experiment Design

Learning designer Yi selects a specific decision point in the course: a particular activity where students are encouraged to reflect on their responses. She defines two conditions for her experiment:

1. Condition 1: No self-explanation prompt is shown to the students.

2. Condition 2: A self-explanation prompt is provided, asking: Can you explain why you chose your answer?

Yi defines the correctness of the student’s answer to a multiple-choice question (related to the activity) as the reward for the experiment. This allows her to measure the impact of reflection prompts on learning outcomes.

---

Comparing Traditional and Adaptive Experiments

Imagine that we ran both a traditional uniformly-randomly assigned RCT and an adaptive experiment in parallel, using the same design, to compare their results.

Results of the Traditional Experiment

In the traditional experiment, there is a statistically significant difference between the mean rewards (where the mean can be interpreted as the share of positive rewards for each condition). The results are as follows:

• Condition 2 (self-explanation prompt): M2=0.608 (SEM=0.032)

• Condition 1 (no prompt): M1=0.512 (SEM=0.032)

Results of the Adaptive Experiment

In the adaptive experiment, the computed estimates were:

• Condition 2 (self-explanation prompt): M2=0.599

• Condition 1 (no prompt): M1=0.539

These results also favor the self-explanation prompt (Condition 2). However, as discussed earlier, the primary advantage of adaptive experiments lies in the allocation of participants to different conditions.

---

Allocation Differences

In the traditional experiment, as expected, participants were assigned almost equally to the two conditions. By contrast, in the adaptive experiment, the assignment proportions differed significantly, reflecting the algorithm’s ability to prioritize better-performing conditions (in this case, Condition 2).

Only 176 students (40%) were assigned to Condition 1 (the worse-performing condition). This means that the algorithm allocated 262 students (60%) to Condition 2, which was identified as the better option according to our analysis. This corresponds to more than a 10% reallocation toward the better-performing condition. It illustrates how adaptive A/B comparisons can facilitate the rapid use of gathered evidence, which is especially relevant in real classroom settings.

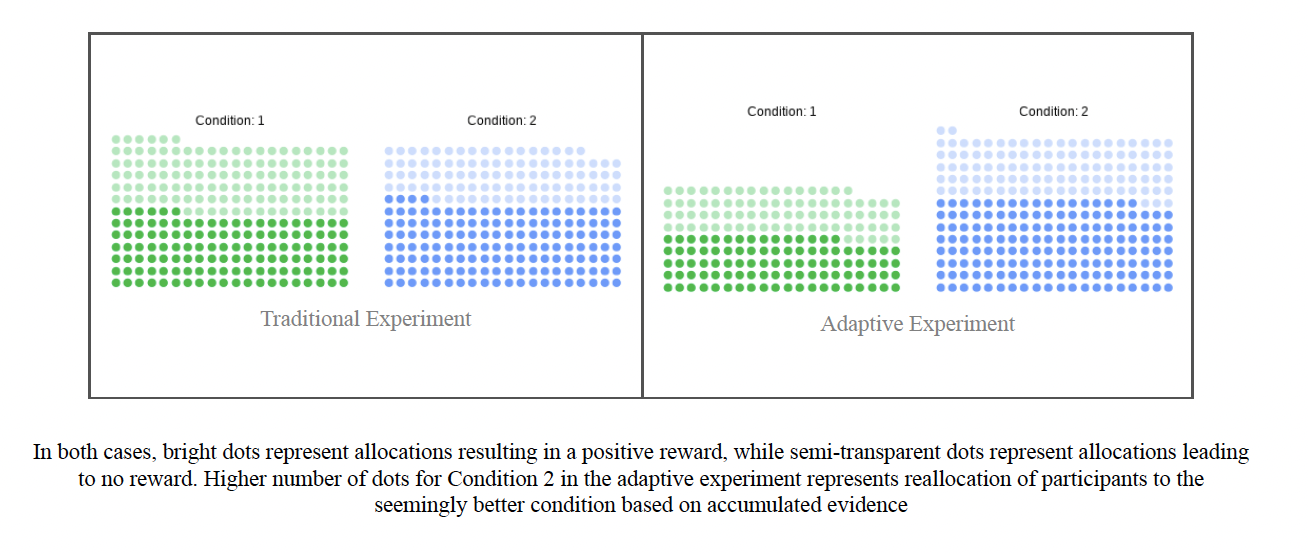
Question:

What is the key benefit of adaptive experimentation compared to traditional Randomized Controlled Trials, as described in the example?

Adaptive experiments assign participants equally to each condition.Adaptive experiments aim for more participants to be assigned to the condition with better outcomes as the experiment progresses.Adaptive experiments are faster to conduct with fewer participants.Adaptive experiments provide statistically significant results without needing a control group.

Adaptive experiments aim for more participants to be assigned to the condition with better outcomes as the experiment progresses:

Explanation of Options:

• Option 1: Incorrect. Unlike traditional RCTs, adaptive experiments dynamically adjust participant allocation based on observed outcomes, rather than assigning participants equally.

• Option 2: Correct. The key benefit of adaptive experimentation is the ability to allocate more participants to conditions with better outcomes, improving efficiency and relevance.

• Option 3: Incorrect. Adaptive experiments may not always be faster or require fewer participants; their primary benefit lies in the adaptive allocation process.

• Option 4: Incorrect. Adaptive experiments still require a control group to compare outcomes and do not bypass statistical requirements for significance.

DID I GET THIS?

Question:

How would you explain an idea of Adaptive Experiment to a child in 150 words or less?

Thanks for Response!

Imagine you’re trying to figure out the best flavor of ice cream for your birthday party, but you don’t know which one everyone likes the most. Instead of giving everyone the same flavor, you start by letting a few people try chocolate and a few people try vanilla. After they taste it, you see which one people like better. If more people like chocolate, you give more chocolate to the next group of friends to try, but you still let some people try vanilla, just in case their opinion changes things.

Over time, you keep adjusting how much chocolate or vanilla you give out based on what people like. By the end, you’ll know which flavor is the best for your party. That’s how an Adaptive Experiment works—it learns as it goes and tries to do better each step!

Question:

If Condition 1 has reward statistics ( S = 2, F = 10 ), and Condition 2 has ( S = 10, F = 2 ), on the next step we:

Are more likely to select Condition 2Will always select Condition 1Are equally likely to select any conditionAre more likely to select Condition 1Will always select Condition 2

Are more likely to select Condition 2:

Explanation of Options:

• Option 1: Correct. Condition 2 has a significantly higher success-to-failure ratio (( S = 10, F = 2 )) compared to Condition 1 (( S = 2, F = 10 )), making it more likely to be selected in the next step.

• Option 2: Incorrect. While Condition 1 is less successful, adaptive experiments use probabilities for selection, and no condition is guaranteed to be selected on every step.

• Option 3: Incorrect. Conditions are not equally likely to be selected, as the selection probabilities depend on observed reward statistics.

• Option 4: Incorrect. Condition 1 has a lower reward ratio compared to Condition 2, so it is less likely to be selected.

• Option 5: Incorrect. Condition 2 is more likely to be selected, but it is not guaranteed to be chosen every time.

The following table displays the results of the experiments:

Experiment	Condition	Successes	Failures
Experiment A	Condition 1	4	6
	Condition 2	6	4
Experiment B	Condition 1	8	12
	Condition 2	12	8

Question:

Compare two experiments based on the table above. In both Experiment A and Experiment B, the success rate for Condition 1 is the same (40%). In both Experiment A and Experiment B, the success rate for Condition 2 is also the same (60%).

We know more about the effectiveness of every condition in Experiment A than in Experiment BWe know more about the effectiveness of every condition in Experiment B than in Experiment AWe know the same amount of information about the effectiveness of every condition in Experiments A and B

We know more about the effectiveness of every condition in Experiment B than in Experiment A:

Explanation of Options:

• Option 1: Incorrect. While Experiment A has fewer participants, the proportional success rates do not provide higher certainty compared to Experiment B.

• Option 2: Correct. Experiment B has a larger sample size, reducing variability and providing more information about the effectiveness of each condition.

• Option 3: Incorrect. Although the success rates are identical, the amount of information differs due to the sample sizes.

Question:

Compare two experiments based on the table above. In both Experiment A and Experiment B, the success rate for Condition 1 is the same (40%). In both Experiment A and Experiment B, the success rate for Condition 2 is also the same (60%).

We are more likely to select Condition 1 in Experiment A than in Experiment BWe are more likely to select Condition 1 in Experiment B than in Experiment AWe are equally likely to select Condition 1 in Experiment A and in Experiment B

We are more likely to select Condition 1 in Experiment A than in Experiment B:

Explanation of Options:

• Option 1: Correct. Experiment A has a smaller sample size, resulting in a posterior distribution with greater variability. This increases the likelihood of selecting Condition 1 compared to Experiment B, where the larger sample size reduces posterior variability and skews the selection toward the true success rates.

• Option 2: Incorrect. In Experiment B, the posterior is more concentrated due to the larger sample size, which reduces the likelihood of selecting Condition 1.

• Option 3: Incorrect. Despite identical success rates, the difference in posterior variability makes the likelihood of selecting Condition 1 different between the experiments.